
こんにちは元塾講師TSUTOMUです。
今回は「中学受験の算数で出題される、特殊算の種類や解き方が知りたい!」という疑問に答えます。
中学受験の算数には、普段の四則演算とは異なる「特殊算」と呼ばれる問題が出題されます。
これらの問題は、創造的な発想や独自の解法が求められる一方で、その解き方を理解すれば効率的に解ける場合もあります。
本記事では中学受験で出題される代表的な特殊算の種類と、それらを解くための具体的な解法を徹底的に解説します。特殊算に苦手意識を持つ小学生にも、スキルアップを目指す小学生にも役立つ情報をお届けします。
さあ、特殊算の世界へ一緒に踏み込んでみましょう!
私がお伝えできること
中学受験における特殊算数の種類と解き方

中学受験における特殊算数の問題には、以下のようなものがあります。
中学受験における特殊算「つるかめ算」

「つるかめ算」は、日本の中学受験において特殊な算数問題の一つであり、文章題の中でも比較的頻出する特殊算です。この特殊算では、つるとかめが交互に進む様子を表現し、その動きに関する問題を解くことが求められます。具体的に解き方を解説します。
【例題】
つるとかめがそれぞれ時速3kmと4kmで対向して出発しました。つるがかめより1時間遅れて出発したとき、二者が出会うのは何時間後ですか?
【解き方】
この問題では、つるとかめの速さの差が1km/h(4km/h – 3km/h = 1km/h)であることに注目します。つるがかめより1時間遅れて出発しているので、二者が出会うまでにつるが1時間分だけ走っていることになります。
二者が出会うまでの時間を「x時間」と仮定。すると、つるはx時間走り、かめはx時間 – 1時間だけ走ることになります。
次に、つるとかめの距離の関係を考えます。出会うときには、つるとかめが合わせて何キロメートル走っていることになるので、つるの距離 + かめの距離 = 合計距離となります。
- つるの距離は時速3kmで走るので、つるの距離は3km/h × x時間 = 3xキロメートルとなります。
- かめの距離は時速4kmで走るので、かめの距離は4km/h × (x時間 – 1時間) = 4(x – 1)キロメートルとなります。
これを合計距離に代入し、方程式を解きます。
3x + 4(x – 1) = 合計距離
合計距離は二者が出会うときに走る距離なので、0となります。
3x + 4(x – 1) = 0
この方程式を解くと、x = 4となります。
よって、二者が出会うのは4時間後です。
つるかめ算は、文章題の中で数学的な論理と計算力を駆使して解く必要がある特殊算のため、慣れるまでは少し難しいかもしれません。しかし、問題を解く過程で論理的思考力と数学の基本的な応用力を養うことができる特殊算なので、繰り返し練習してマスターすることをおすすめします。
中学受験の特殊算「つるかめ算」を解くコツやポイント
中学受験の特殊算「つるかめ算」を解く際のコツやポイントを以下にまとめます。
- 図を描く:「つる」と「かめ」の動きを理解するために、図を描くと役立ちます。二者の動きを時間経過に応じて表現し、問題文に沿って進んでいく様子をイメージします。
- 速さの差を把握する:問題文で「つる」と「かめ」の速さの差が与えられる場合がよくあります。この速さの差をしっかり把握することが重要です。
- 時間を変数化する:二者が出会うまでの時間を「x時間」と仮定すると、問題を解く際に方程式を立てることができます。
- 距離の関係を考える:出会うときには、つるとかめが合わせて走った距離が等しいことに着目します。つるとかめの距離を時間と速さを使って表現し、方程式を立てることで問題を解くことができます。
- 方程式を解く:立てた方程式を解くことで、出会うまでの時間を求めることができます。
- 答えのチェック:得られた答えが問題文と合っているか、再度問題文と照らし合わせて確認します。
「つるかめ算」は論理的思考力と計算力が求められる、中学受験の特殊算です。問題の言い回しや条件を正確に理解し、数学的な知識を応用して解くことがポイント。繰り返し練習し問題に慣れることで、スムーズに解けるようになる特殊算かと思います。また図を描いたり代数的な方法を使っても解くことができるので、中学受験へむけ子供に合った解き方を見つけると良いです。
中学受験における特殊算「和差算・分配算」

和差算
中学受験の特殊算である「和差算」と「分配算」について、具体的な解き方を含めて解説します。
和差算は、数字の和と差を利用して数式を解く問題です。主に二次方程式を扱います。
【例題】
次の二次方程式を因数分解してください。
x^2 + 5x + 6 = 0
【解き方】
この二次方程式を因数分解するために、和差算を利用します。まずこの方程式の項を観察します。
x^2 + 5x + 6 = 0 の中で、x^2と6は互いに和(+)を取り、x^2と5xは互いに差(-)を取ります。
次に、和差算を使って因数分解を行います。
(x + a)(x + b) = x^2 + 5x + 6
aとbを求めるためには、以下のように計算します。
a + b = 5(xの係数が5なので)
a × b = 6(定数項が6なので)
これらの条件を満たすaとbの組み合わせを考えると、a = 2, b = 3 が答えとなります。
したがって、元の方程式を因数分解すると、
(x + 2)(x + 3) = 0
x = -2 または x = -3
となります。
分配算
分配算は、数式の各項に共通の要素を分配することで式を変形する問題です。
【例題】
次の式を分配算を使って展開してください。
2(x + 3)
【解き方】
この式を分配算を使って展開するために、2と(x + 3)の各項に2を分配します。
2(x + 3) = 2 × x + 2 × 3
それぞれ計算すると、
2(x + 3) = 2x + 6
となります。
和差算と分配算は、数式を変形する上で基本的な特殊算テクニックです。理解してマスターすることで、中学受験へむけ高度な特殊算式の変形や方程式の解き方に応用することができます。
中学受験の特殊算「和差算・分配算」を解くコツやポイント
中学受験の特殊算である「和差算」と「分配算」を解く際のコツやポイントを以下にまとめます。
【和差算を解くコツ・ポイント】
- 項の観察:問題の数式をよく観察し、和差算の特徴を把握することが重要です。特に、二次方程式の場合は、x^2と定数項が和や差の形に現れることがよくあります。
- 和差算の利用:和差算を使って数式を因数分解する際には、項を適切にグループ化して和差算を利用します。特に、x^2と定数項の和と差を考えるときに注意してください。
- 式の変形:和差算を適用して数式を因数分解したり、式を変形したりする際には、アルゴリズム的な手順を確認し、正確に計算を行うように心掛けさせてください。
【分配算を解くコツ・ポイント】
- 分配法則の理解:分配算を解くためには、分配法則を理解することが重要です。分配法則は、「a × (b + c) = a × b + a × c」という形で表され、数式の各項に共通の要素を分配することを意味します。
- 正確な計算:分配法則を適用して式を展開する際には、計算の順序や正確さに注意して計算を行わせてください。特に、符号の扱いに注意し、間違いを防いでください。
- 仮定を活用:式を展開する際には、仮定を活用して計算を簡略化することができます。仮定を設定することで、式の中の項を効率的に処理できる場合があります。
和差算や分配算は、数学的な基礎的な操作であり、中学受験で頻出する特殊算です。正確な計算や式の変形が必要となるため、特殊算問題を解く際には集中力を持って取り組むことが中学受験対策として重要です。
中学受験における特殊算「方陣算」

中学受験の特殊算「方陣算」について具体的な解き方を解説します。
方陣算は与えられた数字を正方形の格子状に配置し、行や列の合計値が与えられる場合に各マスの値を求める特殊算問題です。
【例題】
次の方陣の各マスに1から9の数字を入れてください。ただし、行や列の合計値が与えられています。
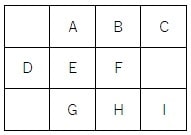
条件:
A + B + C = 15
D + E + F = 10
G + H + I = 18
A + D + G = 16
B + E + H = 13
C + F + I = 12
解き方:
まず、条件に基づいて数式を立てます。
A + B + C = 15
D + E + F = 10
G + H + I = 18
A + D + G = 16
B + E + H = 13
C + F + I = 12
次に、条件4から6を使って各マスの値を求めます。
A + D + G = 16 → A = 16 – D – G
B + E + H = 13 → B = 13 – E – H
C + F + I = 12 → C = 12 – F – I
そして、条件1から3を使ってA, B, C, D, E, F, G, H, Iを求めます。
(16 – D – G) + (13 – E – H) + (12 – F – I) = 15
(16 – D – G) + E + F = 10
G + H + (12 – F – I) = 18
これらの方程式を解くことで、各マスの値を求めることができます。
このように、方陣算では与えられた条件を元に方程式を立て、数学的な計算を行って各マスの値を求める方法を取ります。行列や連立方程式の知識が活用される特殊算のため、しっかりと基礎を理解して取り組むことが中学受験へむけ重要です。
中学受験の特殊算「方陣算」を解くコツやポイント
中学受験の特殊算である「方陣算」を解く際のコツやポイントを以下にまとめます。
- 条件を整理する:方陣算の問題は、与えられた条件をうまく利用して各マスの値を求めることが求められます。まずは、条件をよく観察し、どのような数式や方程式を立てれば各マスの値が求められるかを整理させてください。
- 行と列の合計値を活用する:方陣算では、行や列の合計値が与えられることが一般的です。これらの合計値を利用して各マスの値を求めることが効果的です。特に、行や列の合計値から他のマスの値を求めることができる場合には、その情報を利用して解を進めると良いと思います。
- 仮定を活用する:方陣算の問題では、各マスの値を求める際に仮定を立てることがあります。例えば、Aの値をxと仮定して解を進めるなど、代入法を用いて解を進めることがあります。仮定を活用することで、問題の複雑さを減らすことができる場合があります。
- 正確な計算:方陣算の問題では、正確な計算が求められます。特に、符号の扱いや計算の順序に注意して計算を行ってください。誤った計算が結果に影響を与える可能性があるため、丁寧な計算を心掛けさせてください。
- 練習を重ねる:方陣算は初めての人には難しい場合もありますが、練習を重ねることで慣れることができます。問題集やアプリなどを活用して繰り返し解くことで、問題のパターンやアプローチ方法を理解することができます。
方陣算は与えられた情報をうまく活用し、数式や方程式を立てて解を求める能力が求められる中学受験の特殊算です。中学受験へむけ問題解決力や論理的思考力を養うことが期待できるため、積極的に取り組んで特殊算スキルを向上させてください。
中学受験における特殊算「流水算」

中学受験の特殊算である「流水算」は、数字の流れを考えながら計算を行う問題です。一つの数字から始まり、規則に従って次々に変化していく数字を求めることが求めらる特殊算です。以下に具体的な解き方を解説します。
【例題】
1 → 4 → 7 → 10 → 13 → ?
このような流れを持つ数字列が与えられた場合、次に来る数字を求める問題です。
【解き方】
- 数字の差を観察する:流水算では、数字同士の差に規則性があることが多いです。まずは与えられた数字列をよく観察し、隣り合う数字の差を求めてください。
- 規則性を見つける:数字の差から規則性を見つけます。例題の場合、隣り合う数字の差は3ずつ増えています。このように規則性を見つけることで、次に来る数字を予測することができます。
- 規則を適用して次の数字を求める:規則性を見つけたら、次の数字を求めます。例題では、13 + 3 = 16 となるため、次に来る数字は16となります。
したがって、与えられた数字列の次の数字は「16」です。
流水算は規則性を見つけることが中学受験へむけ重要な特殊算であり、数字の差や倍数などに着目することが効果的です。繰り返し練習を行い、規則性を見つける力を養うことで、中学受験の特殊算「流水算」をスムーズに解くことができるようになります。また流水算は数列の一般項を求める際や、数学の応用問題などでも応用されるため、中学受験対策のみならず様々な場面で役立つスキルとなります。
中学受験の特殊算「流水算」を解くコツやポイント
中学受験の特殊算である「流水算」を解く際のコツやポイントを以下にまとめます。
- 数字の差を観察する:流水算では、数字同士の差に規則性があることが多いです。まずは与えられた数字列をよく観察し、隣り合う数字の差を求めてください。
- 規則性を見つける:数字の差から規則性を見つけます。差が等差数列(等間隔の数列)を成す場合や、等比数列(隣り合う数字の比が一定の数列)になっている場合など、規則性を見つけることが重要です。
- 規則を適用して次の数字を求める:規則性を見つけたら、次の数字を求めます。規則性を利用して次の数字を予測することができます。
- パターンを活用する:流水算にはさまざまなパターンがあります。例えば、等差数列や等比数列の場合は差や比が一定ですが、他にもルールが存在することがあります。繰り返し練習を行い、異なるパターンにも慣れるようにさせてください。
- 変化する部分に着目する:流水算では数字が次々と変化していくため、変化する部分に着目することが重要です。変化する数字の関係性を見つけることで、次に来る数字を予測することができます。
- 繰り返し練習を行う:流水算は慣れが重要な要素です。繰り返し練習を行い、規則性を見つける力を養ってください。問題集やアプリを使って多くの問題に取り組むことで、さまざまなパターンを理解することができます。
流水算は規則性を見つける力や論理的思考力を養うことが期待できる特殊算のため、中学受験へむけ積極的に取り組むことが重要です。また、流水算は中学受験へむけた数学の基礎的なスキルを身につける上での第一歩といえる特殊算でもあります。
中学受験における特殊算「旅人算」

中学受験の特殊算である「旅人算」は、移動する人物や物体の位置や時間を考慮して計算を行う特殊算です。一つの出発地点から移動し、一定の時間や速度で目的地に到着する場合に、途中の位置や所要時間を求める問題が一般的です。以下に具体的な解き方を解説します。
【例題】
AさんとBさんが同じ時刻に出発し、Aさんは時速40kmで、Bさんは時速50kmで向かい合う方向に移動します。AさんとBさんが出発してから2時間後に出会った時、Aさんは何km移動したかを求めよ。
【解き方】
AさんとBさんが2時間後に出会うという情報を活用する:AさんとBさんが2時間後に出会うということから、2時間分の移動距離の合計が出会った地点までの距離になります。
AさんとBさんの移動距離を計算する:AさんとBさんは向かい合う方向に移動しているので、2時間後に出会うまでの移動距離の合計は、Aさんの移動距離とBさんの移動距離の和になります。Aさんの時速は40km、Bさんの時速は50kmなので、Aさんの移動距離は 40km/h × 2h = 80km 、Bさんの移動距離は 50km/h × 2h = 100km です。
Aさんの移動距離を求める:Aさんの移動距離は80kmです。したがって、Aさんは出発してから2時間後に80km移動していました。
中学受験で良く出題される旅人算は、移動する物体や人物の位置や時間を考慮して計算する問題です。時速や移動時間を上手に活用し、移動距離や到着時刻などを求めることが中学受験へむけ重要です。問題文をよく理解し、情報を正確に把握することが解くコツとなります。
中学受験の特殊算「旅人算」を解くコツやポイント
中学受験の特殊算である「旅人算」を解く際のコツやポイントを以下にまとめます。
- 問題文をよく理解する:旅人算は移動する物体や人物の位置や時間を考慮して計算する問題です。問題文をよく理解し、与えられた情報を正確に把握することが重要です。
- 速さと時間の関係を理解する:旅人算では、速さ(時速や分速などの速度)と時間の関係が重要です。移動距離は速さと時間の積で求められますので、速さと時間を正確に組み合わせることがポイントです。
- 時間を揃える:複数の物体が異なる速さで移動する場合、問題を解く際には時間を揃えることが有効です。出発時刻を合わせたり、出会う時間を考えたりすることで、問題をシンプルに解くことができます。
- 図を描く:問題文を読んでイメージがつきにくい場合は、図を描いて視覚的に把握すると良いです。出発地点や目的地、移動する物体の位置などを図に示すことで、問題の構造を理解しやすくなります。
- 単位を揃える:速さや時間の単位が異なる場合は、計算をする前に単位を揃えることが大切です。すべての速さや時間を同じ単位に揃えることで、計算が簡単になります。
- 繰り返し練習を行う:旅人算は慣れが重要な要素です。繰り返し問題を解くことで、速さと時間の関係を理解し、問題に対するアプローチがスムーズになります。
旅人算は日常生活でよく出会う状況を数学的に表したものであり、実生活と結びつけて理解することでこの特殊算に親しみやすくなります。繰り返し練習を通じて速さと時間の計算に慣れ、問題解決力を高めることが中学受験へむけ特殊算対策として大切です。
中学受験における特殊算「通過算」

中学受験の特殊算である「通過算」は、数字を通り抜けながら計算を行う問題です。一つの数字からスタートして、指定された計算を繰り返して最終的な答えを求めることが一般的な特殊算です。以下に具体的な解き方を解説します。
【例題】
通過算を使って、数字3からスタートして3回繰り返し加算し、2回繰り返し減算した後の結果を求めよ。
【解き方】
- 最初の数字を決定する:通過算では最初の数字が与えられています。この例題では最初の数字は3です。
- 加算を繰り返す:指定された回数だけ加算を繰り返します。この例題では3回繰り返すので、3 + 3 + 3 = 9 となります。
- 減算を繰り返す:指定された回数だけ減算を繰り返します。この例題では2回繰り返すので、9 – 3 – 3 = 3 となります。
- 結果を求める:最終的な結果は3になります。
中学受験の特殊算「通過算」を解くコツやポイント
中学受験の特殊算である「通過算」を解く際のコツやポイントを以下にまとめます。
- 問題文をよく理解する:通過算は数字を通り抜けながら計算を行う問題です。問題文をよく理解し、与えられた条件や計算の手順を正確に把握することが重要です。
- 初期値と繰り返し回数を確認する:通過算では最初の数字(初期値)と加算・減算を繰り返す回数が指定されます。問題文を注意深く読み、これらの値を把握させてください。
- 加算と減算の順序を考える:通過算では加算と減算を繰り返す場合があります。計算の順序が結果に影響を与えることに注意して、加算と減算の順序を問題文に応じて適切に判断させてください。
- 計算の手順を整理する:問題文から得られる情報を元に、計算の手順を整理させてください。最初の数字から始めて指定された回数だけ加算・減算を繰り返し、最終的な結果を求めることが目標です。
- 頭の中で計算を行う:通過算は複数の計算を順に行う問題ですが、頭の中で計算を進める能力が求められます。途中の結果を適切に保持しながら計算を進めることがポイントです。
- 繰り返し練習を行う:通過算は数学的な論理思考を養ううえで有用な問題形式です。繰り返し問題を解くことで、計算の手順を把握し、問題解決力を高めることができます。
通過算は数学的な思考力を養う特殊算問題であり、繰り返し練習を通じて慣れることが中学受験へむけ大切です。
中学受験における特殊算「時計算」

中学受験の特殊算である「時計算」は、時計の針の動きを考慮して計算を行う特殊算問題です。通常は時計の針が指す数値や時間の変化を利用して、数値の加算・減算や時間の計算を解決します。以下に具体的な解き方を解説します。
【例題】
時計の針が3時を指している時から、5時間後は何時を指すか求めよ。
【解き方】
- 時計の針の動きを理解する:時計の針は1時間につき360°(一周)回転します。1時間で360°となるため、1時間ごとに360°/12 = 30°だけ進むことになります。
- 1時間ごとの動きを考慮する:時計の針が3時から5時間後の時間を求めるため、まず1時間ごとの動きを計算します。5時間 × 30°/時間 = 150°となります。
- 時計の針を動かす:時計の針が元々3時を指していたため、150°だけ進めると3時 + 150° = 5時となります。
中学受験の特殊算「時計算」を解くコツやポイント
中学受験の特殊算である「時計算」を解く際のコツやポイントを以下にまとめます。
- 時計の針の動きを理解する:時計の針は1時間につき360°(一周)回転します。また、1時間ごとに針の角度は30°進みます。この基本的な動きを理解することが重要です。
- 時間の変化を針の動きに換算する:時計算では、時間の変化を針の動きに換算して計算します。時計の針が何時間で何度動くかを計算し、与えられた時間を針の動きに応じて変換してください。
- 1時間ごとの動きを活用する:時計の針は1時間ごとに30°進むことを利用して、複数時間後の針の位置を求める場合には1時間ごとの動きをかけ算や足し算で計算します。
- 針の位置を計算する際に注意する:針の位置は12時間制の場合、時計の12の位置を0°として、それに対して時計回りに何度進んでいるかで表します。また、24時間制の場合には、針の位置が0°から何度進んでいるかを計算します。
- 頭の中で計算を行う:時計算は頭の中で計算を行うスキルが求められます。途中の計算結果を適切に保持しながら計算を進めることがポイントです。
- 繰り返し練習を行う:時計算は数学的な論理思考を養う問題形式です。繰り返し問題を解くことで、時計の針の動きや時間の変化を把握し、問題解決力を高めることができます。
時計算は日常生活でもよく利用される計算方法であり、実践的な特殊算スキルです。問題集やアプリを使って様々なパターンの時計算に取り組むことで、特殊算攻略へ向け計算のスピードや正確性を向上させてください。また時計の針の動きを視覚的にイメージすることも、中学受験対策として効果的な学習方法です。時計算の基本をマスターし、自信を持って解けるようになることで、中学受験へむけた特殊算対策に役立ちます。
中学受験における特殊算「周期算」

中学受験の特殊算である「周期算」は、数列や周期的なパターンを利用して数値を計算する問題です。通常は周期的な数列の規則性を見つけて、それに基づいて与えられた数値を求めることが求められる特殊算です。以下に具体的な解き方を解説します。
【例題】
次の数列において、第10項を求めよ。
2, 4, 6, 8, 10, 2, 4, 6, 8, 10, …
【解き方】
- 数列の周期を見つける:与えられた数列は2から10までの数字が順に繰り返される周期的な数列です。この場合、周期は5となります。
- 第n項の求め方を確認する:周期性が分かったら、与えられた問題で第10項を求めるために、10 ÷ 5 = 2余り0であることに気付きます。
- 第n項を求める:周期が5であり、10項目は2周期分先の数字に相当します。よって、第10項目は2周期分先の数字である2となります。
中学受験の特殊算「周期算」を解くコツやポイント
中学受験の特殊算「周期算」を解く際のコツやポイントを以下にまとめます。
- 数列の周期を見つける:周期算では、与えられた数列の周期性を見つけることが重要です。数列が何項目ごとに繰り返されるかを見極めることで、解き方が分かりやすくなります。
- 周期を利用して第n項を求める:周期性が分かったら、与えられた問題で第n項を求めるために、nを周期で割った余りを計算します。余りが0であれば、直接周期の先頭の数字が第n項になります。
- 数列の規則性を見つける:周期算では数列の規則性を見つける能力が求められます。数列の項同士の関係や増減の仕方をよく観察し、その規則性を把握することで問題解決に役立ちます。
- 繰り返し練習を行う:周期算は数列の規則性を見つける能力を養う問題形式です。繰り返し問題を解くことで、周期性を見極める力を向上させることが重要です。
- 数列の特殊なパターンにも注意する:周期算には数列の特殊なパターンも含まれることがあります。奇数項と偶数項で規則が異なる、隣り合った項の差が常に同じといった特殊なケースにも注意させてください。
- 視覚的なイメージを持つ:数列の周期を視覚的にイメージすることで、計算がスムーズに行えることがあります。数列のパターンを視覚的に把握する練習も有効です。
周期算は数列の規則性を見つける能力を養う特殊算問題であり、繰り返し問題を解くことで中学受験へむけ理解を深めることが重要です。
中学受験における特殊算「消去算」

中学受験の特殊算である「消去算」は、数式の中に含まれる特定の数字を消去して、新しい数式を作る問題形式の特殊算です。具体的な解き方を以下に解説します。
【例題】
以下の数式から数字「3」を消去し、新しい数式を作れ。
25 + 37 – 13 × 3 + 9 = ?
【解き方】
- 数式を一つずつ計算する:まずは元の数式を左から右に計算していきます。25 + 37 = 62, 62 – 13 = 49, 49 × 3 = 147, 147 + 9 = 156
- 指定された数字を消去する:次に、指定された数字「3」を消去します。この場合、数式中のすべての「3」を消去します。
- 新しい数式を作る:数字「3」を消去した数式は、25 + 7 – 1 × + 9 = 156 となります。
中学受験の特殊算「消去算」を解くコツやポイント
中学受験の特殊算「消去算」を解く際のコツやポイントを以下にまとめます。
- 数式の計算を丁寧に行う:消去算は数式の計算を進めていく問題形式の特殊算です。計算を途中で間違えると、消去するべき数字が見落とされることがあります。数式の計算は一つずつ丁寧に行わせてください。
- 指定された数字をすべて消去する:問題文で指定された数字をすべて消去することが重要です。指定された数字を見落とさないように注意させてください。
- 数式の全体像を把握する:消去算では、数式の全体像を把握することが特殊算を解くポイントとなります。数式を左から右に進めて計算していく際に、どの部分で消去すべき数字が現れるかを把握しておくと効率的に特殊算を解けます。
- 演算子の優先順位に注意する:数式の計算において、演算子の優先順位を理解しておくこともこの特殊算では重要です。掛け算や割り算が加算や減算よりも先に行われるため、計算順序を間違えないようにさせてください。
- 反復練習を行う:消去算は論理的思考力や、計算力を養う特殊算の問題形式です。繰り返し問題を解くことで、数字を正確に消去する力を向上させることが特殊算対策として重要です。
- 計算ミスを防ぐために紙にメモをする:複雑な数式の場合、紙に計算の途中結果や消去すべき数字をメモしておくと、特殊算の計算ミスを防ぐことができます。
消去算は正確な計算力と論理的思考力を養う問題形式の特殊算であり、慣れることで中学受験へむけスムーズに解けるようになります。
中学受験における特殊算「過不足算」

中学受験の特殊算である「過不足算」は、与えられた数式の中に含まれる数値を微調整して正確な答えを導く問題形式の特殊算です。具体的な解き方を以下に解説します。
【例題】
以下の数式の空欄に適切な数値を入れて、等式を完成させよ。
12 + □ – 5 = 25
【解き方】
- 与えられた数式の左辺を計算する:空欄を含む数式の左辺を計算します。例題の場合、12 + □ – 5 = 7 + □ となります。
- 等式を完成させる:与えられた等式の右辺の値が25であることがわかっているため、空欄に入れるべき数値を求めます。例題の場合、7 + □ = 25 となります。
- 空欄に入れるべき数値を計算する:空欄に入れるべき数値は、25から左辺の数値を引いて求めることができます。例題の場合、25 – 7 = 18 となります。したがって、空欄には「18」を入れることで等式が完成します。
中学受験の特殊算「過不足算」を解くコツやポイント
中学受験の特殊算「過不足算」を解く際のコツやポイントを以下にまとめます。
- 等式の左辺と右辺を比較する:過不足算の特殊算では、与えられた等式の左辺と右辺を比較することが重要です。左辺と右辺が等しいことを利用して、空欄に入れるべき数値を求めます。
- 数式の左辺を計算する:空欄を含む数式の左辺を計算します。この段階では、空欄に入れるべき数値を特定せず、まずは数式を整理します。
- 等式を完成させる:与えられた等式の右辺の値が既知の場合、空欄に入れるべき数値を求めます。等式を左辺と右辺で比較し、数値を特定します。
- 空欄に入れるべき数値を計算する:空欄に入れるべき数値は、等式の右辺の値から左辺の数値を引くことで求めます。
- 精度を高めるために紙に計算を書く:複雑な数式の場合、紙に計算の途中結果をメモしておくと、この特殊算で計算ミスを防ぐことができます。
- 反復練習を行う:特殊算の過不足算は正確な計算力や、論理的思考力を養う問題形式です。繰り返し問題を解くことで、数値を正確に微調整する力を向上させることが重要です。
過不足算は計算の精度や、論理思考力を高めるための重要な問題形式の特殊算。繰り返し練習を通じて、とにかく特殊算に慣れることが中学受験へむけ大切です。計算の間違いを防ぐため、紙に計算の途中結果をメモしておくことも有効です。過不足算の基本を押さえ繰り返し練習をすることで、中学受験の特殊算対策に役立ちます。
中学受験における特殊算「倍数変化算」

中学受験の特殊算「倍数変化算」は、与えられた数列の法則を見つけて、次の数を予測する問題形式の特殊算です。具体的な解き方を以下に解説します。
【例題】
次の数列の法則に基づいて、次の数を求めよ。
2, 4, 8, 16, 32, □
【解き方】
- 数列の法則を見つける:与えられた数列をよく観察して、法則を見つけることが第一歩です。例題の場合、各数は前の数を2倍して得られていることがわかります。
- 次の数を予測する:与えられた数列の法則に基づいて、次の数を予測します。例題の場合、最後の数32を2倍して得られる数を求めます。32 × 2 = 64 となるため、次の数は「64」となります。
中学受験の特殊算「倍数変化算」を解くコツやポイント
中学受験の特殊算「倍数変化算」を解く際のコツやポイントを以下にまとめます。
- 数列の法則を見つける:与えられた数列をよく観察し、数値の増減パターンや規則性を見つけることが重要です。数列の中には2倍、3倍、4倍などの定数倍の法則が含まれることが多いので、特にそれらの法則に注目させてください。ただし、複雑な法則も存在することがありますので、慎重に分析してみてください。
- 仮説を立てて検証する:数列の法則を見つける際は、いくつかの仮説を立ててそれを検証することが役立ちます。例えば、数列が2倍に増えているのではないか、3つごとに加算されているのではないか、などの仮説を立てて、それが正しいかどうか確認してみてください。
- 反復練習を行う:倍数変化算は、数列の法則を見つける洞察力や論理的思考力を養う問題形式です。繰り返し問題を解くことで、数列の法則を見つける力を向上させることができます。問題集やアプリを使って様々なパターンの倍数変化算に取り組み、多くの反復練習を行ってください。
- 精度を高めるために紙に計算を書く:複雑な数列の場合、紙に計算の途中結果をメモしておくと、計算ミスを防ぐことができます。数列の法則を見つける際には、手書きで計算をすることでより正確な解答に近づけることができます。
特殊算の倍数変化算は計算の精度、論理思考力を高めるための重要な問題形式です。繰り返し練習を通じて慣れることで、中学受験へむけ数列の法則を見つける能力を向上させてください。問題集やアプリを使って様々なパターンの倍数変化算に取り組むことで、この特殊算における法則を見つける力を高めることが中学受験対策として大切です。
中学受験における特殊算「植木算」

中学受験の特殊算「植木算」は、木の植え方や剪定(せんてい)の方法に関連した問題形式の特殊算です。具体的な解き方を以下に解説します。
【例題】
ある庭に、リンゴの木とオレンジの木を植えることにしました。リンゴの木を3本植え、オレンジの木を4本植えるためには、リンゴの木がオレンジの木よりも2本多くなるように植えるとします。庭に植えるリンゴの木とオレンジの木の合計本数を求めなさい。
【解き方】
- 前提を整理する:リンゴの木を3本、オレンジの木を4本植えるとき、リンゴの木がオレンジの木よりも2本多くなるようにするという条件が与えられています。
- 代数を用いて解く:リンゴの木をx本、オレンジの木をy本とすると、以下の式が成り立ちます。
x = y + 2 (リンゴの木がオレンジの木よりも2本多く)
x + y = 3 + 4 = 7 (リンゴの木を3本、オレンジの木を4本植える) - 方程式を解く:上記の2つの式を用いて、xとyを求めます。
y + 2 + y = 7
2y + 2 = 7
2y = 5
y = 5 ÷ 2 = 2.5 - 解の判定:yが少数になってしまいましたが、木の本数は整数でなければなりません。この場合、条件を満たす整数解はありません。したがって、この問題には解が存在しません。
中学受験の特殊算「植木算」を解くコツやポイント
中学受験の特殊算「植木算」を解く際のコツやポイントを以下にまとめます。
- 条件を代数で表す:植木算では、与えられた条件を代数(変数)を用いて表します。例えば、リンゴの木をx本、オレンジの木をy本として表すなど、木の本数を変数で表してください。
- 方程式を立てる:代数で条件を表現したら、それらを用いて方程式を立てます。木の本数に関する条件や制約を方程式に変換して解きやすい形にしてください。
- 方程式を解く:立てた方程式を解いて、変数の値(木の本数)を求めます。整数解を求める場合、整数でない場合は解が存在しないか、条件を満たす整数解があるか確認させてください。
- 解の判定:求めた変数の値が意味を持つかどうか確認します。木の本数は整数でなければならないため、求めた変数の値が整数でない場合は条件を満たす解が存在しません。
- 適切な方法で解く:植木算には一つの方法だけでなく、いくつかの解法があります。自分にとって理解しやすい方法を選んで解くと良いと思います。
植木算は代数的なアプローチが求められる特殊算問題であり、方程式を解く力や整数解の判定が重要です。問題文をよく読み、条件を的確に代数で表現し、適切な方程式を立てて中学受験へむけ特殊算を解く練習を行わせてください。また、整数解の判定に注意することも中学受験の特殊算対策として重要です。
中学受験における特殊算「平均算」

中学受験の特殊算「平均算」は、平均値を求める問題形式の特殊算です。具体的な解き方を以下に解説します。
【例題】
あるクラスのテストの点数が次のようになっています。
数学:70点、80点、90点、60点、85点
このクラスの平均点を求めなさい。
【解き方】
- 平均点の計算:平均点は、全ての点数の合計を点数の個数で割ることで求めることができます。
- 点数の合計を求める:与えられた点数を全て合計します。
70 + 80 + 90 + 60 + 85 = 385 - 点数の個数を数える:与えられた点数の個数を数えます。
5つの点数があるので、点数の個数は5です。 - 平均点を計算する:点数の合計を点数の個数で割って平均点を求めます。
平均点 = 385 ÷ 5 = 77
中学受験の特殊算「平均算」を解くコツやポイント
中学受験の特殊算「平均算」を解く際のコツやポイントを以下にまとめます。
- 平均点の計算方法を理解する:特殊算における平均算は、平均点を求める問題です。平均点は全てのデータの合計をデータの個数で割ることで求められます。この計算方法を理解させておいてください。
- 問題文を注意深く読む:特殊算の問題文に含まれる情報をよく把握することが重要です。どのデータが与えられているのか、それらの数値は何個あるのかを確認させてください。
- データを整理する:この特殊算は、与えられたデータを整理しやすい形にまとめると解きやすくなります。例えば、点数の合計を計算するために、与えられた点数を全て足し合わせるなどの整理を行わせてください。
- 計算の間違いに注意する:特殊算の平均算は簡単な計算で解ける場合が多いですが、ミスを防ぐために計算を丁寧に行ってください。特に、合計値を求める際に数値を正確に足し算することが特殊算対策として重要です。
- 答えを意味的に確認する:計算が終わった後は、求めた平均点が意味的に正しいか確認させてください。例えば、点数の範囲内に平均点があるかどうか、小数点以下を四捨五入するか切り捨てるかなどを確認させます。
特殊算の平均算は中学受験で頻出する問題であり、基本的な数学の概念を理解していれば解くことができます。問題文を丁寧に読み、計算に慎重に取り組むことが中学受験へむけポイントです。また、計算のステップを順番に進めることで、特殊算における解き方を間違えることなく正確に解くことが期待できます。
中学受験における特殊算「相当算」

中学受験の特殊算「相当算」は、2つの値の相当な量を求める問題形式の特殊算です。具体的な解き方を以下に解説します。
【例題】
ある商品の値段が1000円で、消費税率が10%の場合、消費税込みの価格を求めなさい。
【解き方】
- 消費税額を計算する:消費税額は、商品の値段に消費税率をかけることで求めることができます。
消費税額 = 商品の値段 × 消費税率 = 1000円 × 0.10 = 100円 - 消費税込みの価格を計算する:商品の値段と消費税額を足し合わせることで、消費税込みの価格を求めることができます。
消費税込みの価格 = 商品の値段 + 消費税額 = 1000円 + 100円 = 1100円
中学受験の特殊算「相当算」を解くコツやポイント
中学受験の特殊算「相当算」を解く際のコツやポイントを以下にまとめます。
- 問題文を注意深く読む:この特殊算は、問題文に与えられた情報を正確に把握することが重要です。商品の値段や消費税率、割引率などの数値を確認し、どのような量を求めるべきか理解させてください。
- 割合の計算をマスターする:特殊算の相当算では、割合の計算が頻繁に行われます。消費税率や割引率を小数に変換し、正確に計算できるようにさせてください。割合の計算に不慣れな場合は、繰り返し練習することで特殊算のベクトルに慣れさせることが重要です。
- ステップを順番に進める:相当算は複数の計算ステップを、順番に進めることで解くことができます。ステップを途中で飛ばさず、正確に計算を行わせてください。計算過程を整理するため手書きのメモを取るとよいと思います。
- 小数点の取り扱いに注意する:特殊算における割合の計算では、小数点を適切に取り扱うことが重要です。小数点以下を四捨五入するのか切り捨てるのかを理解し、正確な計算結果を得るようにさせてください。
- 必要な単位を揃える:特殊算の問題文によっては、単位が異なる値が与えられることがあります。計算する前に、必要な単位を揃えることが大切です。
相当算は中学受験の特殊算の一つであり、基本的な割合の計算と順序立てた計算が求められます。中学受験へむけ特殊算の問題文を理解し、計算に慎重に取り組むことで正確な解答を得ることができます。
中学受験における特殊算「日暦算」

中学受験の特殊算「日暦算」は、与えられた日付から日数を計算したり、特定の日数を加減算する問題形式の特殊算です。具体的な解き方を以下に解説します。
【例題1】
2019年4月1日から2019年5月5日までの日数を求めなさい。
【解き方】
- 4月1日から5月1日までの日数を計算する:4月は30日までなので、4月1日から4月30日までの日数は30日です。
- 5月1日から5月5日までの日数を計算する:5月1日から5月5日までの日数は5日です。
- 合計する:30日(4月1日から4月30日までの日数) + 5日(5月1日から5月5日までの日数) = 35日
【例題2】
2019年1月1日から2020年3月31日までの日数を求めなさい。
【解き方】
- 1月1日から12月31日までの日数を計算する:
1年は通常365日ですが、2020年は閏年なので2月が29日あります。
1月1日から12月31日までの日数は、31日(1月)+ 29日(2月)+ 31日(3月)+ 30日(4月)+ 31日(5月)+ 30日(6月)+ 31日(7月)+ 31日(8月)+ 30日(9月)+ 31日(10月)+ 30日(11月)+ 31日(12月) = 365日
2020年1月1日から3月31日までの日数を計算する:2020年は閏年なので、2月が29日あります。
2020年1月1日から3月31日までの日数は、31日(1月)+ 29日(2月)+ 31日(3月) = 91日 - 合計する:365日(2019年の日数) + 91日(2020年の日数) = 456日
中学受験の特殊算「日暦算」を解くコツやポイント
中学受験の特殊算「日暦算」を解く際のコツやポイントを以下にまとめます。
- 月の日数を覚える:特殊算の日暦算では、月の日数を正確に把握することが重要です。一般的な日数は、1月から12月まで順に31日、28日(または29日:閏年)、31日、30日、31日、30日、31日、31日、30日、31日、30日、31日です。これらの日数をしっかり覚えさせてください。
- 閏年に注意する:閏年は通常の年より1日多く、2月が29日になります。閏年は4年に1度やってくるので、特に2月の日数には注意させてください。
- 期間を分割して計算する:長期間の日暦算問題では、年ごとや月ごとに期間を分割して計算することが効果的です。例えば、2年間の日数を求める場合、1年ずつ計算して最後に合計すると間違いが少なくなります。
- 途中の結果を確認する:途中の計算結果を確認しながら進めることで、誤りを早めに見つけることができます。特に閏年の計算や月の変わり目で、日数を誤って計算してしまわないように注意させてください。
- 練習問題を積極的に解く:特殊算の日暦算は、練習を重ねることで慣れることができます。日付を扱う問題を多く解いて、日数の計算をスムーズに行えるようにしてください。
日暦算は中学受験でとくに頻出の特殊算といえる一つであり、計算に正確さと慎重さが求められる問題形式です。中学受験へむけ日数の計算を素早く正確に行えるようになるために、定期的な練習が大切です。特に閏年の計算や月の日数に注意しながら、特殊算問題を解くことで中学受験において高い得点力を身につけることが期待できます。
中学受験における特殊算「やりとり算」

中学受験の特殊算「やりとり算」は、2つの数がやりとりされる操作を繰り返すことで、最終的な答えを求める特殊算問題です。以下に具体的な解き方を解説します。
やりとり算の解き方の一般的な手順は次の通りです。
- 問題文を理解する:与えられた問題文をよく読んで、やりとりされる数値や条件を把握します。問題のポイントを押さえることが解法の第一歩です。
- やりとりの操作を行う:問題文に従って、与えられた数値を操作します。具体的には、指示通りに数値を増減したり、交換したりする操作を繰り返します。やりとりの手順を正確に実行させてください。
- 最終的な結果を求める:すべてのやりとりが終わった後、最終的な結果を求めます。これが問題の答えとなります。
例を用いて解き方を具体的に説明します。
【例題】
ある数が始めは5です。その数を2倍にして3を足し、その後に2をかけて1を引きました。これをもう一度繰り返したとき、最終的な数はいくつでしょうか?
【解法】
始めの数が5です。最初のやりとりでは、5を2倍して10にし、3を足して13になります。
次に、13を2倍して26にし、1を引いて25になります。これが最終的な数です。
したがって、最終的な数は25です。
中学受験の特殊算「やりとり算」を解くコツやポイント
中学受験の特殊算「やりとり算」を解く際のコツやポイントを以下にまとめます:
- 問題文の理解:この特殊算におけるやりとり算の問題は、演算の手順が複雑な場合があります。問題文をよく読み、やりとりされる数値や操作の内容を正確に理解することが重要です。
- 正確な演算:操作の順番や計算を間違えないように注意させてください。特に括弧が含まれる場合は、優先順位を守って計算することが必要です。
- 一つずつ手順を実行する:やりとりされる数値を一つずつ手順通りに実行していくことで、この特殊算では最終的な結果を求めることができます。手順を飛ばさないように注意させてください。
- 途中結果の確認:途中で得られる数値が正しいかどうかを常に確認させてください。誤った数値から計算を続けてしまうと、この特殊算は最終結果が大きくズレてしまいます。
- 練習問題の解答を確認する:問題集などで練習問題を解く際には、解答を確認して正解しているかどうかを確認させてください。間違えた場合は、どこでミスをしているかを理解し、再度取り組むことでこの特殊算の理解を深めることができます。
- 時間配分:受験本番では時間が限られていますので、問題の難易度に応じて適切な時間を割り当てることが重要です。特に複数の計算手順を組み合わせる問題は時間がかかりやすいため、時間配分に気を付けさせてください。
やりとり算は中学受験で頻出の特殊算の一つであり、計算の順番や操作を正確に実行することが求められます。中学受験へむけ問題文の理解力と演算の正確さを養うために、繰り返し練習することがこの特殊算攻略では大切です。慎重に計算を行いながら解法を理解し、解くスキルを高めていくことで、中学受験対策としてやりとり算をスムーズに解くことが期待できるようになります。
中学受験における特殊算「いもづる算」

中学受験の特殊算「いもづる算」は、架空の生物「いもづる」が数列を生成する特殊算問題です。いもづるは「飛び数」と「飛び数の数列」を持っており、それらを使って数列を生成します。具体的な解き方を以下に解説します。
【解き方の手順】
飛び数の決定: まず、「いもづる」が持つ「飛び数」を確認します。この飛び数は問題文に与えられていることが多いです。飛び数は1以上の整数で、いもづるが数列を生成する際にどれだけ数を飛ばすかを表します。
数列の生成: 飛び数を使って数列を生成します。通常、問題文に初項(最初の数)が与えられている場合が多いですが、初項が与えられていない場合もあります。初項が与えられている場合、飛び数を使って順番に数列を作成します。
複雑な数列の場合: いもづる算の問題では、数列が複雑になる場合があります。その場合は、飛び数が途中で変わることがあります。このような場合は、飛び数の変化に気を付けながら数列を生成します。
【具体例】
例として、いもづるが飛び数2で数列を生成する問題を考えます。
【問題】
いもづるが飛び数2で数列を生成します。初項が3の場合、数列の5番目の数を求めなさい。
【解法】
- 飛び数: 飛び数が2で与えられています。
- 数列の生成:
初項: 3
1番目の数: 初項 + 飛び数 = 3 + 2 = 5
2番目の数: 1番目の数 + 飛び数 = 5 + 2 = 7
3番目の数: 2番目の数 + 飛び数 = 7 + 2 = 9
4番目の数: 3番目の数 + 飛び数 = 9 + 2 = 11
5番目の数: 4番目の数 + 飛び数 = 11 + 2 = 13
したがって、数列の5番目の数は13となります。
中学受験の特殊算「いもづる算」を解くコツやポイント
中学受験の特殊算「いもづる算」を解く際のコツやポイントを以下にまとめます。
- 問題文を注意深く読む: 特殊算「いもづる算」の問題文は他の算数の問題と比べてやや複雑な場合があります。問題文を正確に理解するために、注意深く読み取ることが重要です。飛び数や初項が与えられているか、数列の何番目の数を求めるのかなどを把握させてください。
- 飛び数を確認する: 特殊算における「いもづる」が、数列を生成する際に使う「飛び数」を確認します。飛び数は問題文に与えられていることが多いですが、与えられていない場合は自分で読み取る必要があります。
- 数列の生成: 飛び数を使って数列を生成します。通常、初項が与えられている場合は、初項から飛び数を足して順番に数列を作成します。数列の規則性を見つけることが特殊算解答に役立ちます。
- 飛び数の変化に注意する: 特殊算の問題によっては、途中で飛び数が変わる場合があります。飛び数の変化に気を付けて、正確に数列を生成させてください。
- 練習問題を解く: 「いもづる算」は出題頻度は低い特殊算ですが、練習問題を解くことで慣れることができます。繰り返し練習して飛び数や数列の生成に慣れておくと、本番の受験でスムーズに解けるようになります。
- イメージを持つ: 特殊算「いもづる算」は架空の生物が数列を生成する問題なので、イメージを持って解くと理解しやすくなります。いもづるが数列を飛び跳ねるイメージを持ちながら解くのがおすすめです。
中学受験における特殊算の中でも「いもづる算」は比較的出題頻度が低いため、慣れるまでに時間がかかるかもしれません。焦らずに問題文を丁寧に読み、解き方を理解することが中学受験の特殊算対策として重要です。積極的に問題集や過去問を解いて練習し、少しずつ慣れていくことで、中学受験へむけ特殊算問題をスムーズに解く力を身につけることが期待できます。
中学受験における特殊算「エジプトの分数」

分母が1の分数だけを用いて、指定された分数を表現する問題。
エジプトの分数とは、分母が1の分数だけを用いて与えられた分数を表現する方法です。具体的には、与えられた分数を1以下の分数の和として表現します。以下にエジプトの分数を用いた具体的な解き方の例を示します。
【例題】
5/7 をエジプトの分数で表現してください。
【解説」
Step 1: 分子が分母より小さい場合、分母を超えるまで1/分母を繰り返し足します。
5/7 は 1/7 + 1/7 + 1/7 + 1/7 + 1/7 と表現できます。
Step 2: 残った部分を表現します。これは元の分数からすでに足した分数を引いたものになります。
5/7 – 1/7 – 1/7 – 1/7 – 1/7 – 1/7 = 1/7 となります。
よって、5/7 はエジプトの分数で 1/7 + 1/7 + 1/7 + 1/7 + 1/7 + 1/7 + 1/7 と表現されます。
中学受験の特殊算「エジプトの分数」を解くコツやポイント
エジプトの分数は、分母が1の分数だけを用いて与えられた分数を表現する特殊算です。中学受験でエジプトの分数に関する問題が出題されることは稀ですが、エジプトの分数を理解していると数学的な知識として役立ちます。以下に特殊算エジプトの分数を解くコツとポイントをいくつか紹介します。
- 分数を1以下の分数の和に分解する:
特殊算エジプトの分数は、分母が1の分数だけを使って表現するため、与えられた分数を1以下の分数の和に分解します。例えば、5/7 をエジプトの分数で表現する場合、1/7 + 1/7 + 1/7 + 1/7 + 1/7 といったように分解します。 - 最も単純な形にする:
与えられた分数を特殊算エジプトの分数で表現する際には、できるだけ最も単純な形に近づけるようにします。これにより、分母や分子ができるだけ小さい数になり、分数の表現がシンプルになります。 - 他の分数との比較:
特殊算エジプトの分数で表現された分数を他の分数と比較することで、分数の大きさや性質を理解できます。例えば、エジプトの分数で表現された分数が既知の分数よりも大きいか小さいかを確認することができます。 - 分数の足し算・引き算・掛け算:
特殊算エジプトの分数で表現された分数同士の足し算・引き算・掛け算も行うことができます。足し算や引き算では単純に分数を合計したり差を求めたりします。掛け算では分数同士の積を計算します。
中学受験で特殊算エジプトの分数に関する問題が出題されることはあまり一般的ではありませんが、数学の基本的な概念として理解しておくと、数学的な論理や問題解決能力を養う上で役立ちます。
中学受験における特殊算「フィボナッチ数列」

前の2つの数の和が次の数になる数列の問題。
フィボナッチ数列は、最初の2つの数が1で始まり、その後の数は前の2つの数を足した値になる数列です。具体的には、以下のように定義されます。
F(1) = 1
F(2) = 1
F(n) = F(n-1) + F(n-2)(ただし、n ≥ 3)
つまり、フィボナッチ数列は次のように始まります:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …
フィボナッチ数列の特性を利用して、特定の項の値を求める方法について解説します。
【例題】
フィボナッチ数列の第10項を求めてください。
【解説」
フィボナッチ数列の第10項を求めるには、定義に従って順番に計算していきます。
F(1) = 1
F(2) = 1
次に、F(3)を求めます。
F(3) = F(2) + F(1) = 1 + 1 = 2
同様に、F(4)からF(10)までを求めます。
F(4) = F(3) + F(2) = 2 + 1 = 3
F(5) = F(4) + F(3) = 3 + 2 = 5
F(6) = F(5) + F(4) = 5 + 3 = 8
F(7) = F(6) + F(5) = 8 + 5 = 13
F(8) = F(7) + F(6) = 13 + 8 = 21
F(9) = F(8) + F(7) = 21 + 13 = 34
F(10) = F(9) + F(8) = 34 + 21 = 55
したがって、フィボナッチ数列の第10項は55となります。
中学受験の特殊算「フィボナッチ数列」を解くコツやポイント
フィボナッチ数列は、前の2つの項の和が次の項になる数列です。具体的には、最初の2つの項が1で始まり、それ以降は前の2つの項を足した値が次の項となるように進行します。例えば、フィボナッチ数列は次のようになります。1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …
中学受験でフィボナッチ数列に関する特殊算問題が出題されることは、比較的一般的です。以下にフィボナッチ数列を解くコツとポイントをいくつか紹介します。
- 初項と公差の理解:フィボナッチ数列は特殊な数列であり、公差がないことに注意してください。初項は1で、次の項を計算するために前の2つの項を足すだけです。
- パターンを理解する:フィボナッチ数列は特定のパターンに従って進行します。最初の数値から順番に計算していくと、どんどん大きな数が出現していくことに気づくと思います。この特殊算特性を理解することで、フィボナッチ数列の性質を把握することができます。
- 再帰的な性質:フィボナッチ数列は再帰的な性質を持っています。つまり、n番目の項を求める際に、n-1番目とn-2番目の項を求める必要があります。この性質を理解して、順番に計算していくことで任意の項の値を求めることができます。
- パターンを利用した問題解決:フィボナッチ数列に関する特殊算問題は、パターンを利用して解くことが多いです。特定の項の値を求めるだけでなく、項数や項数の範囲に関する問題も出題されることがあります。パターンを活用して問題を解くことで、効率的に解答できる場合があります。
フィボナッチ数列は数学の基本的な概念の一つであり、中学受験の数学における基礎学力を評価する上で重要な要素となります。パターンを理解し、再帰的な性質を把握することで、中学受験へむけ特殊算フィボナッチ数列に関する問題を解くことが期待できるようになります。
中学受験における特殊算「約数の性質」

約数の個数や約数の和に関する問題。
約数(divisor)とは、ある整数を割り切ることができる整数のことを指します。例えば、数値10の約数は1, 2, 5, 10です。
約数の性質にはいくつかの重要な点があります。
- 約数の性質1:ある数の約数は、その数自体よりも大きくなることはありません。
例:数値20の約数は1, 2, 4, 5, 10, 20ですが、20より大きい約数はありません。 - 約数の性質2:すべての整数は、1と自身を約数に持ちます。
例:数値25の約数は1, 5, 25です。1と25は25を割り切ります。 - 約数の性質3:偶数は必ず2を約数に持ちます。
例:偶数8の約数は1, 2, 4, 8です。 - 約数の性質4:奇数の場合、偶数の倍数しか約数に持ちません。
例:奇数15の約数は1, 3, 5, 15です。2, 4, 6, 8などの偶数は約数に含まれません。
約数を求める方法はいくつかありますが、特に大きな数の場合は素因数分解を活用する方法が効果的です。
【例題】
数値36の約数を求めてください。
【解説」
36の約数を求めるために、素因数分解を行います。
まず、36を素因数分解します:
36 = 2^2 × 3^2
次に、すべての約数を求めます。約数は、2の0乗から2の2乗の組み合わせと、3の0乗から3の2乗の組み合わせを掛け合わせたものになります。
1 = 2^0 × 3^0
2 = 2^1 × 3^0
3 = 2^0 × 3^1
4 = 2^2 × 3^0
6 = 2^1 × 3^1
9 = 2^0 × 3^2
12 = 2^2 × 3^1
18 = 2^1 × 3^2
36 = 2^2 × 3^2
したがって、数値36の約数は1, 2, 3, 4, 6, 9, 12, 18, 36です。
中学受験の特殊算「約数の性質」を解くコツやポイント
中学受験で出題される約数の性質に関する問題は、整数の性質や数学的な基本概念を理解していることが重要です。中学受験へむけ、以下に約数の性質を解くコツやポイントをいくつか紹介します。
- 約数の定義を理解する:約数とは、ある整数を割り切ることができる整数のことを指します。例えば、整数Aの約数は、Aを割り切る整数です。約数を求める際には、Aを1からAまでの整数で割ってみることで約数を見つけることができます。
- 約数の個数:ある整数Aの約数の個数を求める際には、Aの素因数分解を利用する方法が有効です。素因数分解によってAを素因数の積に分解し、各素因数の指数に1を足してからそれらを掛け合わせることで約数の個数を求めることができます。
- 約数の性質を利用した問題解決:約数に関する問題は、約数の性質を利用して解くことができる場合があります。例えば、最大公約数や最小公倍数を求める問題では、数の約数を利用して効率的に解くことができます。
- 整数の性質を活用する:約数の問題には、整数の性質や割り算の特性を理解することが役立ちます。特に、偶数や奇数の性質、0の性質、割り算における余りの性質などを理解していると問題解決がスムーズになります。
約数に関する問題は数学の基本的な内容であり、中学受験の数学の試験範囲にも含まれることが多いです。数の性質や割り算の性質を理解し、約数に関する問題を解く際には着実な計算力と論理的な思考力が中学受験へむけ必要となります。繰り返し問題を解くことで、約数の性質をしっかりと理解させておくことが中学受験対策の特殊算攻略として重要です。
中学受験における特殊算「連立方程式」

2つ以上の方程式を解く問題。
連立方程式とは、2つ以上の方程式が同時に成り立つような変数の値を求める問題です。連立方程式を解くためには、2つの方程式をうまく組み合わせて変数の値を求める必要があります。
【例題】
以下の連立方程式を解いてください。
Copy code
2x + 3y = 8
3x – y = 4
【解説」
この連立方程式を解くには、まずどちらかの方程式を変形して、変数の値を消去することを目指します。
方程式2を変形してyを求めます。
3x – y = 4
y = 3x – 4
次に、得られたyの式を方程式1に代入してxを求めます。
2x + 3(3x – 4) = 8
2x + 9x – 12 = 8
11x = 20
x = 20 / 11
xの値が求まったので、この値を方程式2のyの式に代入してyを求めます。
y = 3(20 / 11) – 4
y = 60 / 11 – 44 / 11
y = (60 – 44) / 11
y = 16 / 11
したがって、連立方程式の解は、x = 20/11(約1.82)、y = 16/11(約1.45)となります。
中学受験の特殊算「連立方程式」を解くコツやポイント
中学受験で出題される連立方程式は、2つ以上の方程式が同時に成立する条件を求める問題です。連立方程式を解くためには、以下のコツやポイントを理解しておくと役立ちます。
- 方程式の数を確認する:連立方程式は、2つ以上の方程式が組み合わさっています。問題文をよく読み、与えられた方程式の数を確認させてください。2つの方程式であれば2次元平面上の交点を求めることに相当し、3つ以上の方程式であれば3次元空間上の交点を求めることになります。
- 方程式の種類を理解する:連立方程式には一次方程式(直線)と二次方程式(曲線)などがあります。方程式の種類に応じて、解法や解の求め方が異なります。特に中学受験レベルでは一次方程式の連立方程式が主に出題されます。
- 代入法・消去法を使い分ける:連立方程式を解く際には、代入法や消去法など、さまざまな解法があります。代入法では片方の方程式を解いてその解を他の方程式に代入して解を求めます。一方、消去法では2つの方程式を適切に組み合わせて変数を消去し、残った1つの方程式を解く方法です。問題の難易度や形式に応じて適切な解法を選択させてください。
- 正確な計算を心がける:連立方程式の解を求める際には、正確な計算が求められます。特にマイナス符号や分数の計算を間違えないように注意させてください。計算ミスを防ぐために、段階的に計算を進めることや、答えを元の方程式に代入して確認することが有効です。
- 考察や図示を活用する:連立方程式を解く際には、問題文や図示から得られる情報を活用することも重要です。問題の条件を把握し、方程式に変換する前に問題の意図を理解することが解の導出に役立ちます。
これらのポイントを理解しておくと、中学受験で出題される連立方程式の問題を解く際にスムーズに対応が期待できるようになります。繰り返し問題を解くことで慣れを増し、中学受験へむけ解法の幅を広げることが大切です。
中学受験における特殊算「剰余の性質」

剰余演算に関する問題。
剰余(remainder)とは、ある整数を別の整数で割った際の余りのことを指します。剰余は、割り算の結果における余り部分を表します。剰余の性質にはいくつか重要な点があります。
- 剰余の性質1:剰余の範囲
ある整数を別の整数で割った余りは、常に0以上割る数未満の値になります。例えば、5を3で割った余りは2です(5 ÷ 3 = 1 余り 2)。 - 剰余の性質2:剰余の加法性
ある整数を別の整数で割った余りを、それぞれ別の整数で割った余りの和として求めることができます。つまり、(a + b) ÷ c の余りは、a ÷ c の余りと b ÷ c の余りを足したものに等しいです。 - 剰余の性質3:剰余の乗法性
ある整数を別の整数で割った余りを、それぞれ別の整数で割った余りの積として求めることができます。つまり、(a * b) ÷ c の余りは、a ÷ c の余りと b ÷ c の余りをかけたものに等しいです。
剰余の性質を活用して、剰余の計算を簡単に行うことができます。特に、大きな整数の剰余を計算する際には、これらの性質を上手に利用することで効率的な計算が可能です。
【例題】
123456を7で割った余りを求めてください。
【解説」
剰余の性質を利用して計算を行います。
123456 ÷ 7 = 17636 余り 4
したがって、123456を7で割った余りは4になります。
中学受験の特殊算「剰余の性質」を解くコツやポイント
中学受験で出題される剰余の性質に関する問題は、割り算の余りに関する性質を理解し、計算を効率的に行う能力が求められます。以下に剰余の性質を解くコツやポイントをいくつか紹介します。
- 剰余の定義を理解する:剰余とは、ある整数を別の整数で割った際に生じる余りのことを指します。例えば、10 ÷ 3の場合、商は3で余りは1となります。この余りの1が剰余です。
- 剰余の性質を理解する:剰余にはいくつかの性質があります。例えば、整数Aを整数Bで割った余りがCである場合、A + BやA – BをBで割った余りもCになります。また、A × BをCで割った余りは、(Aの剰余 × Bの剰余)をCで割った余りと等しいです。
- 剰余を利用した計算:剰余の性質を利用して問題を解くことができます。例えば、大きな数を割る問題や連続する数を割る問題では、剰余の性質を使って計算を効率的に進めることができます。
- 逆の操作を考える:剰余を使った計算では、割り算の逆の操作である掛け算を利用することが多いです。ある数の剰余を求める際には、その数に何を掛けていくつ足すと元の数に戻るかを考えると効果的です。
- 計算ミスを防ぐ:剰余を使った計算では、剰余を取ることで値が小さくなる場合があります。計算途中で値が非常に小さくなると、計算ミスのリスクが高まります。計算ミスを防ぐために、計算の途中結果を整数でなるべく大きく保つよう心がけさせてください。
剰余の性質を理解し、計算の際に適切に活用することで、中学受験で出題される剰余の問題をスムーズに解くことができます。中学受験へむけ慣れを増やすためにも繰り返し問題を解くことが重要です。
中学受験における特殊算「確率」

イベントの確率を求める問題。
確率(probability)は、ある事象が起こる可能性の程度を数値化したものです。確率は0から1までの値を取ります。0の場合はその事象が絶対に起こらないことを示し、1の場合はその事象が必ず起こることを示します。
確率を計算する際には、以下の公式を利用します。
確率 = 事象が起こる場合の数 / 全体の場合の数
【例題】
6面のサイコロを振った場合、3が出る確率を求めてください。
【解説」
6面のサイコロを振る場合、出る目は1から6までの整数です。したがって全体の場合の数は6です。
次に、3が出る場合の数を求めます。サイコロの目は1から6までの6通りありますが、その中で3が出るのは1通りだけです。
したがって、3が出る確率は次のように計算できます。
確率 = 事象が起こる場合の数 / 全体の場合の数
確率 = 1 / 6 ≈ 0.1667
よって、サイコロを振った際に3が出る確率は約0.1667(16.67%)です。
中学受験の特殊算「確率」を解くコツやポイント
中学受験で出題される確率の問題は、イベントの起こりやすさを数値化して求める問題です。以下に確率を解くコツやポイントをいくつか紹介します。
- 確率の定義を理解する:確率とは、ある事象が起こる確率を0から1の間の数値で表したものです。0は起こらない確率、1は必ず起こる確率を意味し、0に近づくほど起こりにくく、1に近づくほど起こりやすいです。
- 確率の求め方を理解する:確率を求める際には、そのイベントが起こる場合の数を全体の場合の数で割ることで計算します。例えば、サイコロを振って1が出る確率を求める場合、1が出る場合の数は1で、全体の場合の数は6です。したがって、確率は1/6となります。
- 複数のイベントの確率を求める:複数のイベントが同時に成り立つ確率を求める場合、それぞれのイベントの確率を掛け合わせます。例えば、コインを2回投げて2回とも表が出る確率を求める場合、表が出る確率は1/2で、2回とも表が出る確率は(1/2) × (1/2) = 1/4となります。
- 対立するイベントの確率を利用する:イベントAが起こる確率をpとすると、イベントAが起こらない確率は1 – pです。逆に、イベントAが起こらない確率をqとすると、イベントAが起こる確率は1 – qです。この性質を利用して、特定のイベントが起こる確率を求めることができます。
- 何が求められているかを把握する:問題文をよく読み、何が求められているかを正確に把握することが大切です。例えば、確率を求めるだけでなく、逆に確率から何回試行すれば特定のイベントが起こるかを求める中学受験問題もあります。
これらのポイントを理解し繰り返し問題を解くことで、中学受験へむけ確率の計算力や理解力を高めることができます。特に確率の問題は直感的に理解しにくいことがあるため、問題を解く際には慎重に計算を行い、中学受験へむけ論理的な思考を養うことが重要です。
中学受験における特殊算「等差数列と等比数列」

一定の公差または公比を持つ数列に関する問題。
等差数列と等比数列は、数列の特別なパターンを持つ数列です。中学受験へむけ、具体的に解き方を含めてそれぞれについて解説します。
等差数列(Arithmetic Sequence)
等差数列とは、隣り合う項の差が一定である数列のことを指します。一般的な等差数列は、以下のように表現されます:
a, a + d, a + 2d, a + 3d, …
ここで、aは最初の項(初項)、dは公差(隣り合う項の差)です。
【例題】
初項aが3で公差dが4の等差数列の第5項を求めてください。
【解説」
等差数列の第n項は一般的に以下の式で表されます。
第n項 = 初項 + (n – 1)×公差
第5項を求めるためにn=5として計算します。
第5項 = 3 + (5 – 1) × 4
第5項 = 3 + 4 × 4
第5項 = 3 + 16
第5項 = 19
よって、等差数列の第5項は19です。
等比数列(Geometric Sequence)
等比数列とは、隣り合う項の比が一定である数列のことを指します。一般的な等比数列は、以下のように表現されます:
a, a * r, a * r^2, a * r^3, …
ここで、aは最初の項(初項)、rは公比(隣り合う項の比率)です。
【例題】
初項aが2で公比rが3の等比数列の第4項を求めてください。
【解説」
等比数列の第n項は一般的に以下の式で表されます。
第n項 = 初項 * 公比^(n – 1)
第4項を求めるためにn=4として計算します。
第4項 = 2 × 3^(4 – 1)
第4項 = 2 × 3^3
第4項 = 2 × 27
第4項 = 54
よって、等比数列の第4項は54です。
等差数列と等比数列は数学や物理、経済などの様々な分野で重要な役割を果たしており、数列の性質を理解することで中学受験へむけたさまざまな応用が可能です。
中学受験の特殊算「等差数列と等比数列」を解くコツやポイント
中学受験で出題される等差数列と等比数列は、数列の性質や次の項の値を求める問題がよく出題されます。以下に解くコツやポイントをいくつか紹介します。
等差数列について
- 初項と公差を理解する:等差数列は、一つ前の項に常に同じ数(公差)を加えることで次の項が得られる数列です。初項と公差を把握することが解く上での第一歩です。
- n番目の項の求め方:n番目の項を求める際には、初項に公差を(n-1)回加えることで求めることができます。式で表すと、n番目の項 = 初項 + (n-1) * 公差 となります。
- 項数の求め方:与えられた等差数列の初項、末項、公差を使って、項数を求めることがあります。項数を求める際には、次の式を使います:項数 = (末項 – 初項) / 公差 + 1
等比数列について
- 初項と公比を理解する:等比数列は、一つ前の項に常に同じ数(公比)を掛けることで次の項が得られる数列です。初項と公比を把握することが解く上での基本です。
- n番目の項の求め方:n番目の項を求める際には、初項を公比の(n-1)乗で求めることができます。式で表すと、n番目の項 = 初項 × (公比)^(n-1) となります。
- 項数の求め方:与えられた等比数列の初項、末項、公比を使って、項数を求めることがあります。項数を求める際には、次の式を使います:項数 = log(末項 / 初項) / log(公比) + 1
一般的なポイント
- 問題文をよく読む:与えられた問題文をよく読んで、どのような数列が与えられているのか、何を求めるのかを把握することが重要です。
- 式をうまく使う:数列の性質を理解していると、式を使って問題を解くことが効率的に行えます。特に等差数列や等比数列の性質を活用して問題を解決させてください。
- パターンを見つける:数列には規則性があります。パターンを見つけ、それを利用して次の項を求める方法もあります。
これらのポイントを把握し繰り返し問題を解くことで、中学受験へむけ等差数列と等比数列に対する理解と計算力を向上させることが期待できます。
中学受験における特殊算「立方体の切断」

立方体を平面で切断したときの断面の数や形に関する問題。
立方体の切断は、立方体を平面で切断したときにできる断面の形を理解する問題です。立方体は6つの正方形の面を持つ立方体を指します。平面で立方体を切断すると、様々な形の断面が現れます。
立方体の切断の具体的な解き方を、以下の例題を用いて説明します。
【例題】
立方体を1つの平面で切断したとき、できる断面の形を述べてください。
【解説」
立方体を1つの平面で切断すると、立方体のどの辺を切るかによって断面の形が異なります。一般的な場合として、以下のような断面の形が考えられます:
- 正方形:立方体の中心を通る平面で切断した場合、正方形の断面が得られます。
- 長方形:立方体の辺を斜めに切断すると、長方形の断面が得られます。
- 三角形:立方体の1つの角を通る平面で切断した場合、三角形の断面が得られます。
- 凸多角形:立方体の辺の中点を通る平面で切断すると、凸多角形の断面が得られます。
- 凹多角形:立方体の角を通る平面で切断すると、凹多角形の断面が得られます。
立方体をどのような平面で切断するかによって、断面の形が大きく異なります。また、立方体の切断においては、平面と立方体の辺や角の位置関係が重要な役割を果たします。さまざまな立方体の切断を考えることで、立体の性質を理解することが期待できます。
中学受験の特殊算「立方体の切断」を解くコツやポイント
中学受験で出題される立方体の切断に関する問題は、立方体を特定の方法で切断した際の図形や面の性質を求める問題です。中学受験へむけ、以下に解くコツやポイントをいくつか紹介します。
- 立方体の性質を理解する:立方体は6つの正方形の面から構成されており、対面の面は平行で等しい大きさです。立方体の対角線の交点を中心に対称な面を持つことも特徴です。立方体の性質を理解することで、切断による新しい図形や面の性質を予測することができます。
- 立方体の切断面の形を把握する:立方体の切断面の形によって、新しくできる図形の種類や面の数が変わります。立方体をどのような方向や位置で切断しているのかを正確に把握することが重要です。
- 立体図形の展開図を描く:立方体の切断によってできる新しい図形を把握するために、立体図形の展開図を描くことが役立ちます。展開図を描くことで、切断後の面の配置や形を見やすくなります。
- パターンを見つける:立方体の切断に関する問題には、パターンを見つけることが役立つ場合があります。特定の条件を満たす図形の性質や面の数に関するパターンを見つけると、問題を解く際に効果的なアプローチが見つかることがあります。
- 空間的なイメージを持つ:立方体の切断は空間的な問題であり、図形の立体的なイメージを持つことが解くコツとなります。立方体を実際に手で作ってみたり、想像力を駆使して図形を回転・移動させる練習をすることで、空間的な理解力が向上します。
これらのポイントを考慮し、繰り返し問題を解くことで、中学受験へむけ立方体の切断に対する理解と解決力を高めることが期待できます。立方体の性質と空間的なイメージをしっかりと把握することが、中学受験へむけた立方体の切断問題を解く鍵となります。
中学受験における特殊算「数の性質」

奇数・偶数、素数、完全数などに関する問題。
数の性質には様々なものがありますが、ここでは代表的な数の性質についていくつか解説します。
- 偶数と奇数の性質
偶数は2で割り切れる整数であり、奇数は2で割り切れない整数です。偶数と奇数の性質により、偶数同士または奇数同士の和は必ず偶数になります。また、偶数と奇数をかけると必ず偶数になりますが、奇数同士をかけると結果は奇数になります。 - 素数の性質
素数は1と自身以外の正の約数を持たない数です。2以上の整数の中で、2つの約数しか持たない数が素数です。例えば、2, 3, 5, 7, 11などが素数です。素数は無限に存在し、素数同士をかけると必ず新しい素数が得られることが知られています(素数の乗法的性質)。 - 完全数の性質
完全数は、自身を除く約数の和が自身と等しい数です。例えば、6は1 + 2 + 3 = 6となるため、6は完全数です。完全数には限りがあり、完全数が見つかった数は比較的少ないです。 - 三角数の性質
三角数は、等差数列の一般項の和に相当する数のことを指します。n番目の三角数は、n(n+1)/2で表されます。例えば、1番目の三角数は1、2番目の三角数は3(2 + 1)、3番目の三角数は6(3 + 2 + 1)です。
これらは数の性質の一部ですが、数学には数々の興味深い性質が存在します。数の性質を理解することで、数学の問題を解く際に有益な知識となります。また、数の性質は数学の応用や理論を深める上で重要な基礎となる概念でもあります。
中学受験の特殊算「数の性質」を解くコツやポイント
中学受験で出題される「数の性質」に関する問題は、整数や小数の性質を理解し、数学的な基本的な概念を駆使して解く必要があります。以下に解くコツやポイントをいくつか紹介します。
- 整数の性質を理解する:整数の性質を把握することが中学受験へむけ重要です。例えば、偶数と奇数の性質、約数と倍数の関係、負の数同士の計算、ゼロの特別な性質などを理解しておくと問題を効率的に解くことができます。
- 小数の性質を理解する:小数に関する性質も把握することが中学受験へむけ重要です。小数点の位置や有限小数と循環小数の性質、小数同士の計算などについて理解しておくと問題をスムーズに解くことができます。
- 指数や累乗の性質を利用する:指数や累乗の性質を理解すると、問題を簡単に解くことができる場合があります。特に平方根や立方根の性質を活用することで、計算を簡略化できることがあります。
- 式を変形する:数の性質に関する問題は、式を変形することで解答を導くことができることがあります。代数的な変形を行い、問題文に与えられた条件を式に落とし込むことで問題を解決する方法が中学受験へむけ有効です。
- 図を描く:数の性質に関する問題は、図を描いて視覚的に理解することで解答のアプローチが見えることがあります。特に幾何学的な問題では図を描くことが中学受験へむけ役立ちます。
- 繰り返し問題を解く:数の性質に関する問題は反復練習が中学受験へむけ有効です。繰り返し問題を解くことで、性質や特徴をしっかりと理解し、スキルを向上させることが期待できます。
これらのポイントを考慮し、問題解決のための基礎力を身につけることが中学受験へむけ重要です。数学の基本的な概念と性質を理解し、それらを応用する力を高めることで、中学受験で数の性質に関する問題を自信を持って解くことができます。
中学受験における特殊算「立方根や平方根の近似値」

無理数の近似値を求める問題。
立方根や平方根の近似値を求める際には、いくつかの近似手法を使って計算できます。以下に中学受験へむけ、代表的な近似手法を具体的な例とともに解説します。
ニュートン法による平方根の近似
ニュートン法は、ある方程式の解を近似的に求める方法です。平方根の近似にも使うことができます。平方根の近似値xを求める場合、次のような反復計算を行います。
- Step 1: 初期値としてxを設定します(xの初期値は平方根の近似値として使われます)。
- Step 2: 反復計算により新しいxの値を求めます。
新しいx = (x + S / x) / 2 (ここでSは求めたい平方根の数値)
この反復計算を何度か繰り返すことで、より正確な近似値を得ることができます。
【例題】
√10の近似値をニュートン法を用いて求めてください。
【解説】
初期値としてx = 3(任意の値)を設定します。
反復計算により新しいxの値を求めます。
新しいx = (3 + 10 / 3) / 2
新しいx ≈ 3.1667
次に、新しいxの値を使って再度反復計算を行います。
新しいx = (3.1667 + 10 / 3.1667) / 2
新しいx ≈ 3.1623
これを繰り返し行うと、xの値が収束し、近似値として3.1623を得ることができます。
二分法による平方根の近似
二分法は、ある方程式の解を範囲を絞りながら近似的に求める方法です。平方根の場合、範囲を絞るために平方数を利用します。
例題:√10の近似値を二分法を用いて求めてください。
【解説】
√10は3と4の間にあることが分かっています。したがって、範囲を3から4までに絞ります。
中間値を求めます。中間値 = (3 + 4) / 2 = 3.5
3.5の2乗は12.25で、これは10より大きいです。したがって、√10は3から3.5の間に存在します。
次に、範囲を3から3.5に絞ります。
中間値を求めます。中間値 = (3 + 3.5) / 2 = 3.25
3.25の2乗は10.5625で、これは10より小さいです。したがって、√10は3.25から3.5の間に存在します。
このようにして範囲を狭めながら、より正確な近似値を得ることができます。
立方根の場合も、ニュートン法や二分法などを応用して近似値を求めることができます。これらの手法は近似値を求める際に非常に便利です。
中学受験の特殊算「立方根や平方根の近似値」を解くコツやポイント
中学受験で出題される立方根や平方根の近似値を求める問題は、計算力と近似の方法を使いこなす能力が求められます。中学受験へむけ、以下に解くコツやポイントをいくつか紹介します。
- 重要な近似値を覚える:特定の数の平方根や立方根の近似値は、暗記しておくことで解く速度が向上します。例えば、2の平方根は約1.41、3の平方根は約1.73、2の立方根は約1.26などの近似値は覚えておくと便利です。
- 近似の方法を理解する:立方根や平方根の近似値を求める方法として、二分法や平均法などの近似手法を理解すると役立ちます。特に二分法は、近似の範囲を狭めていく方法で、手計算で近似値を求める際に有効です。
- 比較法を使う:既知の数の平方根や立方根と近い値を求める際には、比較法が有効です。例えば、求めたい数の近くにある整数の平方や立方を利用して近似値を求めることができます。
- 計算の段階を減らす:立方根や平方根の計算は複雑なため、計算の段階を減らすことが近似の精度向上につながります。分数形式から小数形式に変換する、約分する、小数点以下を丸めるなどの方法を使って効率的に計算させてください。
- 実際に計算して確認する:立方根や平方根の近似値を求める際には、最後に実際の計算結果と近似値を比較して確認することが大切です。誤差が許容範囲内に収まっているかを確認することで、近似の正確性を確保します。
これらのポイントを意識して立方根や平方根の近似値を求める練習をすることで、近似のスキルと計算力が向上し、中学受験での問題解決に役立てることができます。

これらは特殊算数の一部であり、中学受験の試験範囲に含まれることがあります。これらの問題は論理的な思考や数学的なアプローチを駆使して解くことが求められるので、練習を通じて慣れておくのがおすすめ。中学受験へむけに向けてしっかりと準備させてください。
中学受験の算数「特殊算」におすすめの問題集5選

中学受験 ミラクル算数 特殊算

「特殊算」25単元を3ステップで完璧に攻略できる書籍です。丁寧な解説と高品質の練習問題、特殊算における発展問題で偏差値アップをサポートしてくれるので、自信を持って中学受験に臨めます。受験生だけでなく、算数の教え方に悩む保護者や家庭教師にも最適な内容。著者は早稲田大学法学部卒で、中学受験指導歴30年以上のベテラン講師。その経験を生かし、会場模試や問題集の執筆も行っています。受験生のことを第一に考え、志望校合格まで強力にサポートしてくれる頼れる存在です。
灘中・開成中・筑駒中受験生なら必ず解いておくべき算数101問

名門私立中学の算数入試問題は学校教科書では対処できないレベルですが、この本は中学受験へむけ過去問対策前にマスターしておくべき基礎的要素と入試最高峰の問題をコンパクトにまとめています。他の参考書と違い、解説がシンプルでわかりやすいのが特徴です。仕事算やニュートン算、水問題など、基本ルールを活用した特殊算問題がたくさんあります。問題数は少ないですが、算数の効率性が披露されており、非常に好感が持てる一冊だと感じました。忙しい子供にも適しているので、中学受験へむけ準備に役立つと思います。
中学入試 実力突破 塾プラス算数文章題

この参考書では、中学受験へむけつまずいた箇所を反復演習することで実戦力を養います。中学入試で頻出の分野を8章に分け、つまずき診断→パワーアップ問題→チャレンジ問題の3段階で取り組みます。つまずき診断では苦手な問題を見つけ、それをパワーアップ問題で克服し、さらにチャレンジ問題で中学受験へむけ特殊算などの実力を高めます。中学受験難関校の入試問題を使っているので、実際のテストに対応できる特殊算知識やテクニックを身につけられます。
さらに、プロ家庭教師からのアドバイスで問題の解き方のコツを学べます。入試問題をどう攻略するか、自分ひとりでは気づかないコツがわかるので中学受験へむけ非常に役立ちます。
また、別冊の解答編も詳細でわかりやすい解説があります。正解できなかった問題もしっかり理解できるので、中学受験へむけ自己学習にも最適です。この参考書は自分の弱点を克服し、中学受験へむけ特殊算などの実力を高めるための強力なサポートとなると思います。
中学入試 算数 塾技100

この参考書は、現役塾講師が塾だけで教える算数の「塾技」を公開しています。難関中学受験の基礎固めに最適で、特殊算など入試頻出の解法パターンが1冊で学べます。わかりやすさと使いやすさを追求し、中学受験へむけ短期間での巻き返しも可能になります。
この本の特長は、受験算数の全単元が一冊にまとまっている点です。他の参考書は分冊であることが多く、結局複数冊買わなければならないことがありますが、この本は幅広い内容を程よい厚さの一冊に収めており中学受験へむけ非常に使いやすいです。
また、ただ公式を並べただけでなく背景や解き方も詳しく解説されているため、中学受験へむけ暗記だけではなく特殊算など本当の算数を学ぶことができます。受験生や算数指導に関わる方には特におすすめの一冊です。
中学入試 見るだけで解き方がわかる受験の算数

中学受験の算数問題は、図を使って考えると面白いほど解けるようになることを実感しました。
この本は、中学受験へむけどれだけ算数が苦手でも大丈夫だというメッセージがあります。落ちこぼれてしまった生徒たちの「つまづき」を取り除き、逆転合格を目指すための裏ワザが大公開されています。中学受験へむけ基礎固めから特殊算など入試直前の巻き返しまで、あらゆる場面で役立つテクニックが詰まった参考書です。
著者は1950年生まれで、数学専門塾「ピタゴラス」を主宰しています。長年にわたり数学の個人指導を行い、学校や大手塾でつまずいた子どもたちを「苦手」から「得意」へと変えてきた指導法で知られています。地元関西の名門校を中心に多くの教え子を合格に導いた経験から、短時間で簡単に理解できる数学・算数のマスター法を数多く発表し、特殊算をはじめ子どもから大人まで好評を博しています。
中学受験の算数「特殊算」におすすめの通信教育3選

中学受験の算数「特殊算」におすすめの通信教育は、間違いなく「マンツーマン指導」というスタイルです。
通信教育には大きく3つのスタイル(紙・デジタル・マンツーマン指導)があり、もし「紙」「デジタル」というスタイルを選んでも中学受験の特殊算まで学ぶことはできません。
その理由は、通信教育スタイルの特性により学べる内容が異なるため。
「紙」「デジタル」は固定式の通信教育で、教科書範囲は学べてもそれ以上の自由度はまったくなし。その反面「マンツーマン指導」は講師との対面式学習となり、教科書範囲外における算数「特殊算」なども自由に学べるという特性があるため。

したがって中学受験の算数「特殊算」は、
間違いなく「マンツーマン指導」の通信教育がベスト&一択です。
![]()
中学受験「特殊算」おすすめ通信教育①オンライン家庭教師 e-Live
| おもな特徴 |
|
中学受験の算数「特殊算」対策として、まず優秀でおすすめのマンツーマン指導がこれ。
2010年にスタートした会社のため知名度はまだ高くないですが、運営している内容については極めて優秀で信頼のおけるもの。
とくに講師陣については、誰でも彼でも採用せず「紹介制」が用いられることで国内トップレベル。
Webサイトの講師紹介ページを見てもわかるように、高学歴・高スキル・高指導力の人材のみ在籍していることが分かるかと思います。

オンライン家庭教師 e-Liveのイメージ
当然ながら中学受験の経験者も多く、算数の特殊算対策についてもバッチリ可能。
その実力もあって少しずつ人気も出てきているマンツーマン指導で、さらに月1回のみの受講も可能という使いやすさも相まって、特殊算対策をはじめ中学受験へむけ利用する家庭も増えつつあるオンライン家庭教師です。
中学受験の算数や特殊算をはじめ、どんなん教科でも対策可能。
全国の志望校データを備えているため目標へ向け特化型のマンツーマン指導が可能で、小学生にぴったりの家庭学習が期待できるかと思います。
もしマンツーマン指導で迷ったら、まず第一候補にする価値ありです。
 ☑ こちらから「無料体験受講」ができます。
☑ こちらから「無料体験受講」ができます。
参考:オンライン家庭教師イーライブ(e-Live)の口コミレビュー
中学受験「特殊算」おすすめ通信教育②学研オンライン家庭教師
| おもな特徴 |
|
中学受験の算数「特殊算」を攻略するのに、この学研マンツーマン指導もかなりおすすめ。
全般的にクオリティが高く、中学受験の経験者も多い講師陣により、算数対策はもちろん特殊算攻略についても分かりやすい指導が期待できます。
過去の合格実績もかなり豊富で、難関校をはじめとする中学受験へ成功した小学生も多数あり。
もともと訪問型の家庭教師を運営していたことで全国の志望校データも豊富にそろえており、子供の目標に特化したマンツーマン指導で人気のある通信教育です。
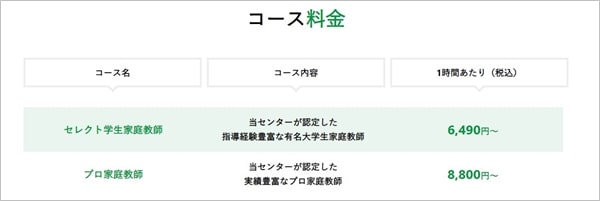
学研オンライン家庭教師の料金体系(一部)
費用面においても良心的で、大手の家庭教師といえば料金に問題がある場合も多いですが、この学研の場合はその点においても安心の料金体系。
大手の家庭教師会社としては不明な費用項目もなく、健全で安心の料金という部分もメリットです。
さすがの学研クオリティで信頼性は極めて高く、しっかりと子供の中学受験対策をはじめ、特殊算攻略としてもおすすめのオンライン家庭教師。
中学受験の算数をはじめ特殊算対策、また総合的な受験勉強として有意義なマンツーマン指導です。
 ☑ こちらから「無料の資料請求」などができます。
☑ こちらから「無料の資料請求」などができます。
中学受験「特殊算」おすすめ通信教育③トウコベ
| おもな特徴 |
|
中学受験へむけ算数対策および特殊算攻略として、かなり効果が期待できるマンツーマン指導の通信教育。
この「トウコベ」という名称は、東大生によるオンライン個別指導から名づけられています。
東大生の指導により余裕の特殊算対策が期待でき、中学受験の算数だけではなく総合的で、より実用的なマンツーマン指導となっていることで人気。
さらに講師&学習プランナー体制によって、しっかりと志望校対策が期待できるオンライン個別指導です。
サポート体制についても求めているスタイルそのもので、24時間いつでも質問できるため極めて学習効率が高まるかと。この「いつでも質問できる」というスタイルは小学生にとって安心感が大きく、どんどん疑問解消できる有意義なメリットかと思います。

トウコベのイメージ
もちろん講師は中学受験の経験者も多く、算数をはじめ特殊算対策はバッチリ。
返金保証もあるため親としても安心できるシステムとなっており、クオリティの高い講師陣とともに極めて効果的な中学受験対策が期待できるマンツーマン指導です。
東大式勉強法というのは表面だけではなく、しっかりと根拠ある実用的な内容。
したがって中学受験にむけた算数対策をはじめ特殊算攻略、さらに全教科においてハイレベルで効果的なマンツーマン指導が期待できる通信教育です。
このトウコベを選ぶのもいいですよ。
 ☑ こちらから「無料の資料請求」などができます。
☑ こちらから「無料の資料請求」などができます。
参考:オンライン家庭教師「トウコベ」の中学受験へむけた対応力を徹底調査!
中学受験の算数「特殊算」おすすめ通信教育まとめ

中学受験算数の特殊算におすすめの通信教育を、まとめ比較一覧で示します。
各サービスをクリックすると、先ほどの各解説項目へジャンプします。
| サービス | おもな特徴 |
| オンライン家庭教師 e-Live |
|
| 学研オンライン家庭教師 |
|
| トウコベ |
|
中学受験の特殊算を解くための思考方法

中学受験の特殊算を解くための一般的な思考方法を以下にまとめます。
- 問題文をよく読む
中学受験へむけ、特殊算の問題文を正確に理解することが解く上で非常に重要です。問題文の意味や条件を理解し、その特殊算で何が求められているのかを明確に把握させてください。 - 与えられた情報を整理する
特殊算の問題文から与えられた情報を整理して整数や式として表現することで、中学受験へむけ問題解決の手がかりを得ることができます。 - パターンを見つける
特殊算の問題には、規則性やパターンが存在することがあります。中学受験へむけパターンを見つけて応用することで、問題を効率的に解くことができる場合があります。 - 代数的な変形を活用する
特殊算の問題は、代数的な変形を行って解くことが有効なことがあります。中学受験へむけ式を変形することで、問題の条件を表現しやすくなります。 - 近似値を用いる
中学受験へむけ特殊な計算を行う場合、近似値を使って問題を簡略化することができることがあります。例えば、平方根や立方根の近似値を使って問題を解決する特殊算方法があります。 - 図を描く
幾何学的な特殊算の問題では、図を描くことで問題の構造を理解しやすくなります。図を描いて視覚的に考えることで中学受験へむけ解決の糸口が見つかることがあります。 - 過去の知識を活用する
中学受験へむけ特殊算の問題は時折、過去に学んだ知識を活用して解くことができることがあります。過去の学習内容を思い出し、中学受験へむけ応用することが大切です。 - 練習を重ねる
中学受験における特殊算の問題は、慣れることで解けるようになるものもあります。繰り返し問題を解くことで、中学受験へむけ特殊算に対するスキルを高めさせてください。

これらの思考方法を駆使して特殊算の問題に取り組むことで、中学受験の数学の問題をスムーズに解決する力を身につけることが期待できます。
中学受験の算数「特殊算」の種類&解き方徹底解説!まとめ
中学受験の算数において「特殊算」は、普段の四則演算とは一線を画し、創造的な発想や独自の解法が求められる問題です。本記事では代表的な特殊算の種類と、それらを解くための具体的な解法を徹底的に解説しました。
これらの特殊算に関する知識と解法を習得することで、中学受験の数学に対する自信と理解が深まるかと思います。
繰り返し問題を解くことでスキルを向上させ、問題解決能力を高めることをお勧めします。
ぜひ中学受験へむけた特殊算の解き方として参考にしてみてください。




